Paid
The best Apps, Games, Mods, Apks, Software, News
for you in one place.
Trending content
Trending games
Trending apps
Top downloads
CapCut
Free
–4.45.6M Downloads
Grand Theft Auto V - Unofficial
Free
465.36 MB4.312.2M DownloadsROBLOX
Free
180.57 MB4.44.1M DownloadsDownloader by AFTVnews
Free
–4.4391.1K DownloadsCx File Explorer
Free
15.04 MB4.2552.7K DownloadsFortnite
Free
241.16 MB4.53.4M DownloadsCall of Duty: Warzone
Free
–3.9153.5K Downloads
News

Safeguarding Your Digital Life with Kaspersky Premium

WhatsApp intends to integrate a phone dialer into its application

Google Maps will expand the use of generative AI and bring it to Labs

This famous emulator will not reach the App Store for an important reason.
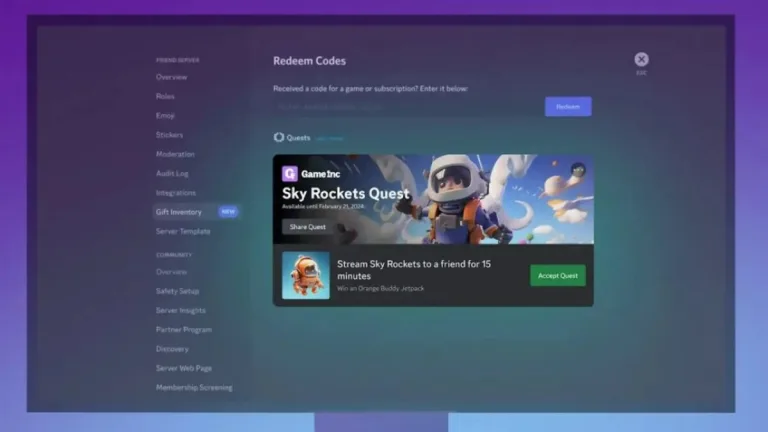
This is the way you can remove Discord ads without paying for Nitro
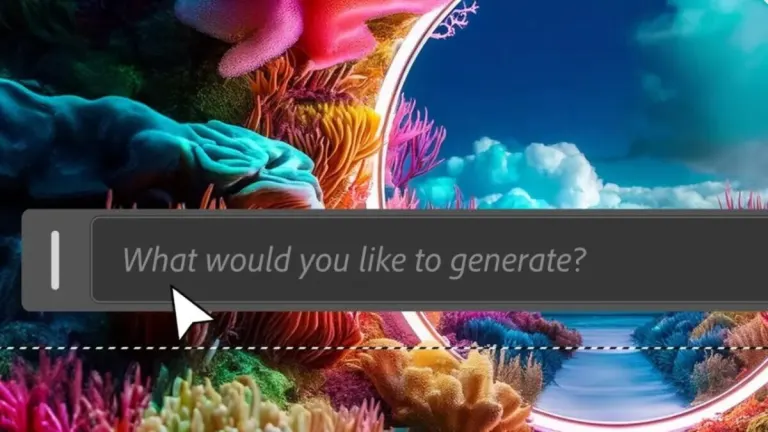
The new artificial intelligence features of Adobe Photoshop will make your life much easier.

Sony patents Auto-Play, a mode that will allow PlayStation players to complete games… without playing?

NASA has just hacked a 1977 satellite that was on Pluto.
Most popular categories
Latest games

Motorcycles of the Apocalypse
- 4.9
- Free

Five Nights at Freddy's: In Real Time
- 4.2
- Demo

Stewie Tweaks Essentials INI
- 4.5
- Free
INI fixes and quality of life improvements for Fallout 3

Bellwright
- 4.8
- Paid
An immersive survival RPG with strategy-based elements

Risky Chronicles and the Curse of Destiny
- 4.4
- Paid

Kill It With Fire 2
- 4.7
- Paid
Ultimate Ludo Game Online
- 4.7
- Free
Ultimate Ludo Game Online
Save Paw - Help Dog Bad Bees
- 4.5
- Free
Save Paw - Help Dog Bad Bees
Легендариум
- 4.8
- Free
Fantasy IDLE RPG Adventure: Легендариум
Puppy newborn pet care salon
- 4.2
- Free
Puppy Newborn Pet Care Salon Overview
Pirates Business
- 4.2
- Free
Pirates Business: Thrilling Pirate Adventure
Saveiro Tuning Pursuit
- 4.5
- Free
Saveiro Tuning Pursuit Overview

Five Nights at Freddy's: In Real Time
- 4.2
- Demo

Pilgrims
- 4.2
- Paid

Gas Station Simulator - Airstrip DLC
- 4.3
- Paid

Gas Station Simulator - Party Time DLC
- 4.3
- Free

Gas Station Simulator - Can Touch This DLC
- 4.3
- Paid
An add-on content for Gas Station Simulator

The Mystery Of Woolley Mountain
- 4.6
- Paid
Step into the enigmatic world of Woolley Mountain
Critters Cat Skins For MCPE
- 4.9
- Free
Critters Cat Skins For MCPE Overview
Addition Math Master 2
- 4.7
- Free
Addition Math Master 2: Speedy Addition Training
Golf is Hard
- 4.3
- Free
Golf is Hard Overview
Pet Party Mahjong
- 4.2
- Free
Pet Party Mahjong: Classic Matching Puzzle Game
Ranch Simulator 23 Build Farm
- 4.4
- Free
A free app for iPhone, by Saif Ullah.
Linked Lines
- 4.8
- Free
Linked Lines Game Review
Latest apps

ISL Online
- 4.5
- Trial version
ISL Online: Secure, Versatile Remote Desktop for All Business Sizes

AltTunes
- 4.7
- Trial version
AltTunes for Windows — an alternative to iTunes designed to be the best backup manager and data transfer tool for your iPhone

Remotly
- 5
- Free
The most secure remote desktop software

iBackup Extractor
- 4.5
- Trial version

Microsoft Clipchamp
- 4.9
- Free
Elevating the art of visual storytelling

Mullvad VPN
- 4.9
- Free
A privacy-first VPN solution
Fintraffic Mobiili
- 4.2
- Free
A free program for Android, by Liikenteenohjausyhtiö Fintraffic Oy.
Minimal Rainbow Color watch 4
- 4.9
- Free
Minimal Rainbow Color Watch Face for Wear OS
Icárion App
- 4.5
- Free
A free program for Android, by W2MDevops.
12 Hindi Book NCERT
- 4.9
- Free
12 Hindi Book NCERT Overview
TCL TV Screen Mirroring
- 4.6
- Free
TCL TV Screen Mirroring App Overview
Alan Walker Songs Offline
- 4.7
- Free
Alan Walker Songs Offline Overview

Mullvad Browser Extension (Firefox)
- 4.9
- Free
Check the status of your VPN quickly

Mullvad VPN
- 4.9
- Free
A privacy-first VPN solution

Mullvad Browser
- 4.9
- Free
A browser to ensure online privacy

LMMS
- 4.8
- Paid
A free and powerful music production tool

Autopano
- 3.4
- Trial version

Enigma Messenger
- 4.1
- Free
A secure and versatile messaging platform
Paris Métro: Subway Driving
- 4.2
- Free
Paris Métro: Subway Driving Overview
Lu Period Tracker Ovulation
- 4.8
- Free
Lu Period Tracker Ovulation
NiceClock Analog
- 4
- Free
NiceClock Analog: Beautiful Analog Clock for iPhone
Freedom Chevrolet San Antonio
- 4.2
- Free
Freedom Chevrolet San Antonio
Yamaha WaveRunners
- 4.1
- Free
Yamaha WaveRunners Overview
Electronic Wooden fish
- 4.1
- Free
Electronic Wooden Fish: Stress Relief App
